What’s the use of math? – a JWST example

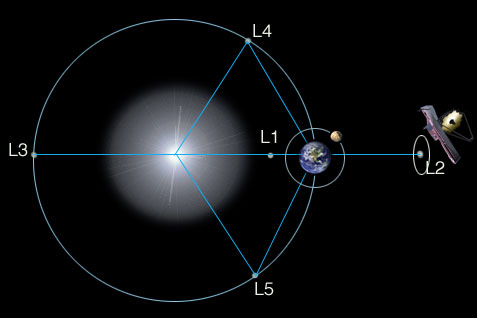
The James Webb Space Telescope will orbit something called L2, discovered thanks to math in an era where only sheep (and a duck and a rooster) flew. (Courtesy NASA)

My 12-year-old daughter, as 12-year-old daughters do, asked me what’s the use of math. I wrote a book about space engineers. Their work is the manifestation of math. I have taken to answering with something along the lines of “math gives us the ability to model the universe and everything in it. And it keeps bridges from falling down on us.”

If we’re in a vehicle when she asks what the use of math is, I might add, “It keeps the wheels from falling off this car.” Recently, I did a story, yet unpublished, about a steel research center at the Colorado School of Mines. One of its co-founders mentioend offhand that there are 11 types of structural steel in nose of a car’s frame, all for a specific reason. He showed me this video of a 1959 Chevy Bel Air crashing head-on into a 2009 Chevy Malibu. The difference in the wreckage, to no small degree, was math.

Yesterday, reading a bit about the Hubble Space Telescope’s 25th anniversary, I came upon a great pure-math example. It has to do with the JWST, not to be confused with SxSW.

The James Webb Space Telescope, Hubble’s successor planned for launch in October 2018, will look farther into the universe’s history than Hubble or any other telescope. It will do more to figure out potentially habitable planets orbiting distant suns, too. It will do all sorts of other stuff to clarify the universe’s development and our place in it. It will cost about $9 billion. Ball Aerospace, the company I wrote about, did up the 18 gold-coated super-lightweight beryllium mirrors, which will unfold into a 21-foot primary mirror.

The JWST will rely on an infrared detector, which has to be kept super-cold. They had to find just the right spot for it in space. The mission designers chose the second Lagrange point (a.k.a. L2), about a million miles away – roughly four times the distance from Earth to the moon. They weren’t the first mission designers to have done this.

From the JWST web page about its future orbit (emphasis mine):

The L2 orbit is an elliptical orbit about the semi-stable second Lagrange point. It is one of the five solutions by the mathematician Joseph-Louis Lagrange in the 18th century to the three-body problem. Lagrange was searching for a stable configuration in which three bodies could orbit each other yet stay in the same position relative to each other. He found five such solutions, and they are called the five Lagrange points in honor of their discoverer.

Lagrange was a contemporary of the Montgolfier brothers. The outer limits of aerospace innovation in those days involved a sheep, a duck and a rooster in a hot air balloon. Lagrange wasn’t looking for applications, couldn’t have conceived of a space telescope. He was just doing math.